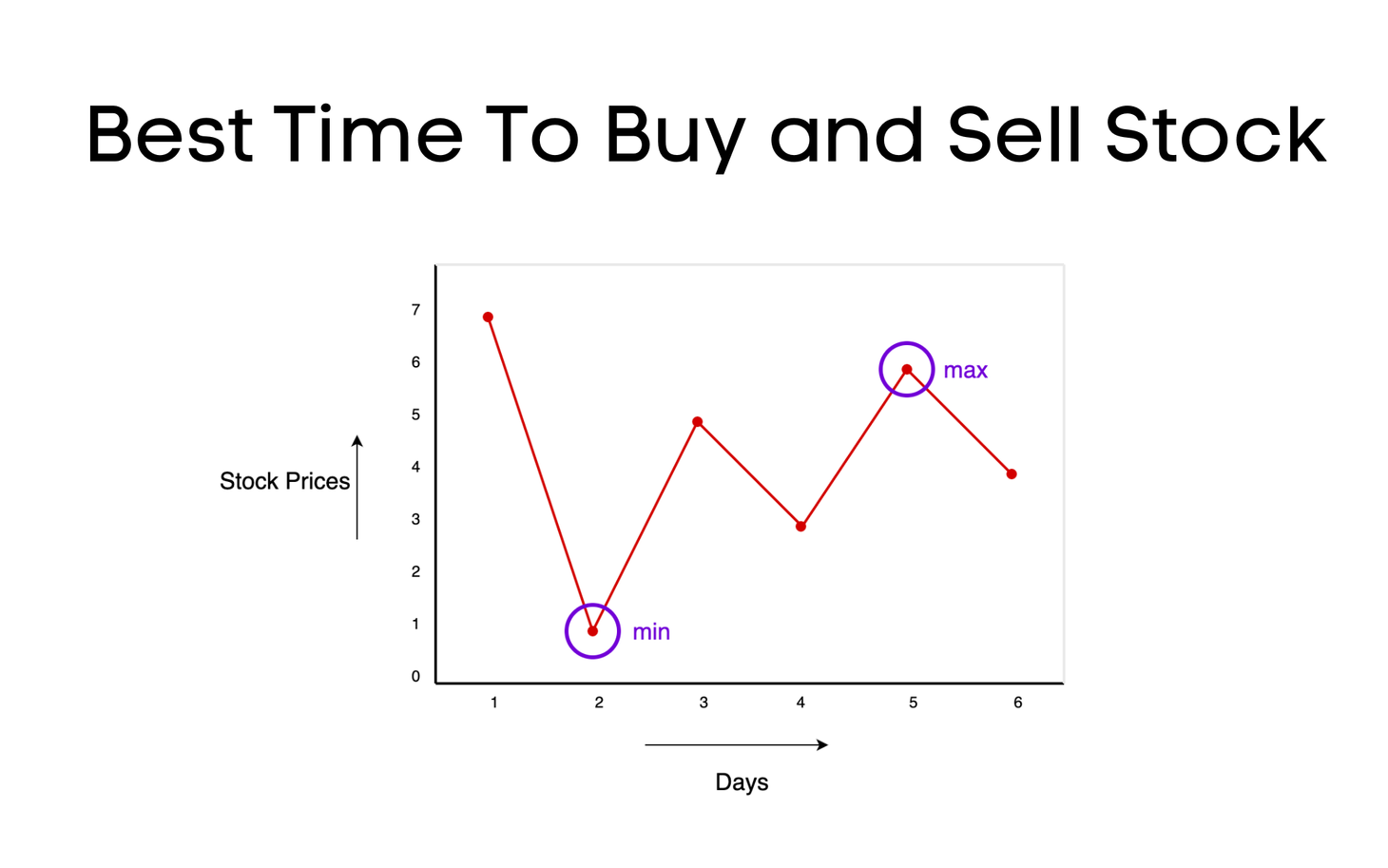
Leetcode 121: Best Time To Buy and Sell Stock
Course Overview "Arrays Mastery For Coding Interviews" is a comprehensive program designed to provide an in-depth understanding of arrays, a fundamental data structure in computer science. The course covers various topics, including array manipulation, multi-dimensional arrays, dynamic arrays, and common algorithms. Students will learn through theoretical lessons and
This lesson will teach you how to find the duplicate element using a hashing algorithm.
