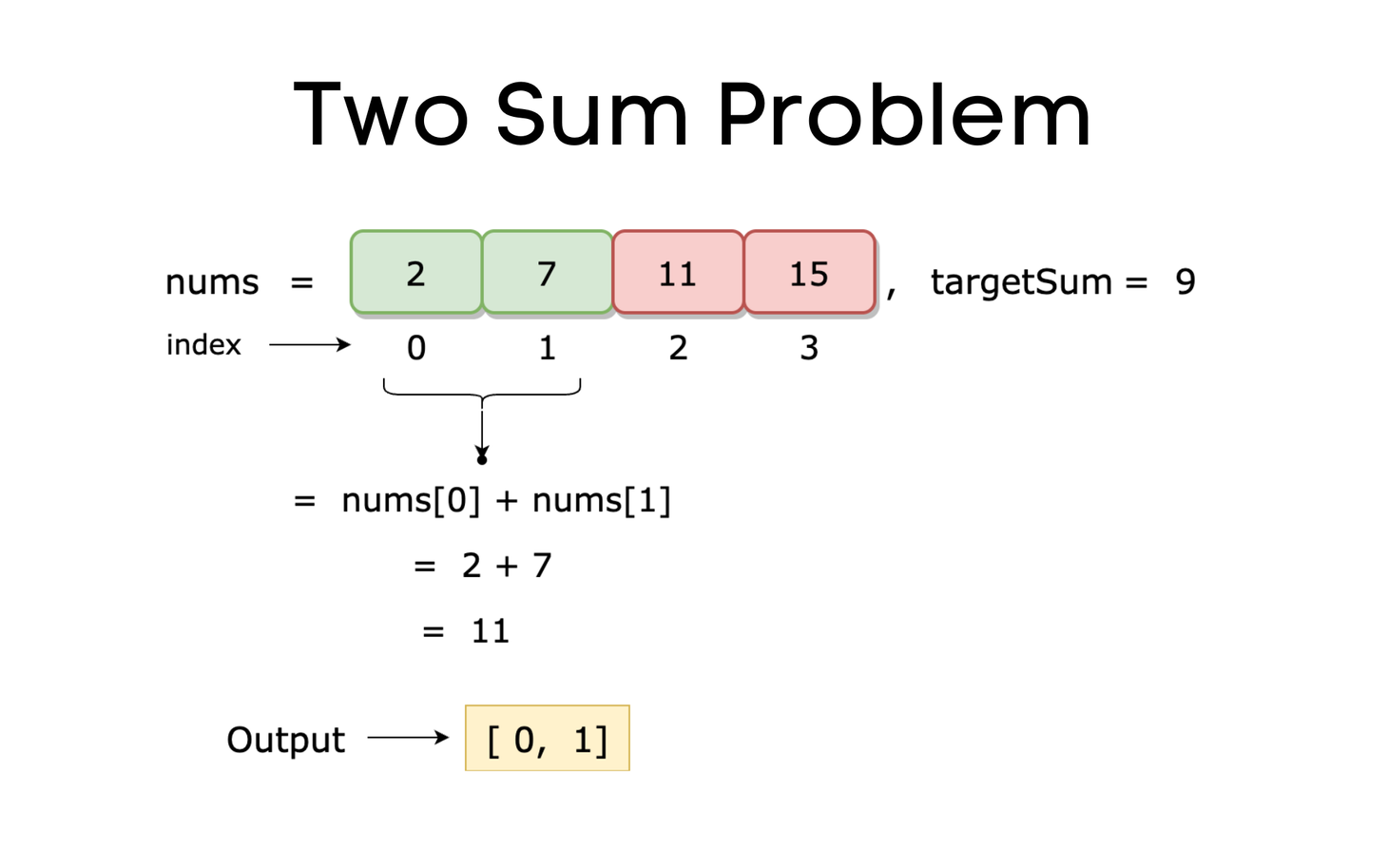
Leetcode 1: Two Sum Problem
This lesson on "Two Sum" coding problem is discussed thoroughly with illustrations and various approaches with running time complexities.
Leetcode 217: Contains Duplicate
This lesson will teach you how to find the duplicate element using a hashing algorithm.